资讯详情

排列组合是国家公务员考试的必考题型，也是绝大部分文科考生所畏惧的，但困难和机遇并存，排列组合考点繁多，每一种模型对应相应解法，若能熟悉其特点，必能在考试时快速准确解出，取得相应分数。专家希望通过以下讲解，帮助考生掌握隔板模型，增强对公考数学的信心。

隔板模型本质为相同元素分不同堆的问题，这类问题的描述类似于：把6个苹果

分给甲乙丙三个不同的小朋友，每个小朋友至少一个的分法总共有多少种?那么可以假设6个苹果站在甲乙丙三个人的前面，只要在6个苹果中间插入两个相同的板那么就可以把苹果分成三堆，其中第一堆默认分给甲，第二堆默认分给乙，第三堆默认分给丙，根据两个板插入位置的不同，各种分法都能够出现，所以总的分法就为：5个空当中插入两个板，即为 。拓展一下即为：把n个相同元素分给m个不同的对象，每个对象至少1个元素，则有 种不同分法。

例1：某单位订阅了 30 份学习材料发放给 3 个部门，每个部门至少发放 9 份材料。问一共有多少种不同的发放方法?

A.7 B.9 C.10 D.12

【解析】

此题为相同元素分推问题，为第一种变形题，其所不同的公式中的使用条件为至少1个，此题为至少9个，故不能直接套用。那么需要转化，第一步要均分到三个部门的材料数为83=24(份)，因为材料一样，分法数为1种;第二步转化为30-24=6份分3个部门，至少1个，则方法数为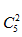 =10，选C。

例2：刘老师有 10 支一模一样的铅笔，想要分给四个学生，他还没有想好每个学生分几支，问刘老师可能的分法有几种?

A.285 B.286 C.287 D.288

【解析】

此题为相同元素分推问题，为第二种变形题，其所不同的公式中的使用条件为至少1个，此题为至少0个，故不能直接套用。那么需要转化，第一步为向4个学生的都借1支，因为材料一样，借法数为1种;第二步转化为10+4=14份分3个部门，至少1个，则方法数为 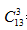=286，选B。

我们在考试中经常碰到此类隔板模型，需要对题目进行适当转化，使之变成大家常见的形式，就能简化运算达到快速解题的目的，专家希望考生能够多总结，再不断辅以练习，相信这类题型将不再是大家备考路上的拦路虎。

以上就是查字典大学网为同学们带来的“2017国考行测备考：巧解排列组合之隔板模型”内容了，希望看完能够带给大家一些力量，对同学的生活有所启示，更多内容在这里，请继续关注我们。